Nature-Inspired Algorithms for iGaming Fraud Detection

iGaming involves the direct financial resources of players, who aim to entertain themselves and increase their wealth. One of the most challenging problems in this field is detecting various fraud issues. Companies spend vast amounts of resources on iGaming antifraud systems to detect technical problems with equipment, cheating behavior by players, possible vulnerabilities, bugs, and security issues.

Finding vulnerabilities as quickly as possible is crucial not only from the company's point of view. Possible fraud issues can worsen the players' experience as well, leading to bugs or discontinuities in the game. However, it is often difficult to find a vulnerability before the real attack occurs, leading to significant losses of resources (financial, reputational, temporal, etc.). The approaches discussed throughout the article significantly reduce the risk of game vulnerability being exploited.

Fraud Detection Challenges in iGaming and Research Objectives

One of the main goals of this article is to present ways for a new monitoring system that allows changing the point of view for fraud detection and detecting vulnerabilities in real-time or, at least, before the real attack leads to significant losses [1]. The challenge lies in detecting fraud in crash games[2] where RTP (Return to Player) can exceed 1 for certain coefficients over long distances. The solution involves a simulation-based approach, using a simulation-based RTP exploit detection algorithm to identify the issue before real damage occurs.

Let us consider the following situation. Suppose there is a game with different coefficients changing from 0 to 20 (for example, crash games like Aviator). Let us also suppose that the game mechanics are incorrect, so the Return to Player (RTP) can be higher than 1 for some coefficients over long distances (for example, due to discontinuity in the coefficient increasing mechanics). Still, it is correct on average (see Fig. 1, for example). However, the players don't know this vulnerability, but it will be discovered sooner or later.

Fig 1:

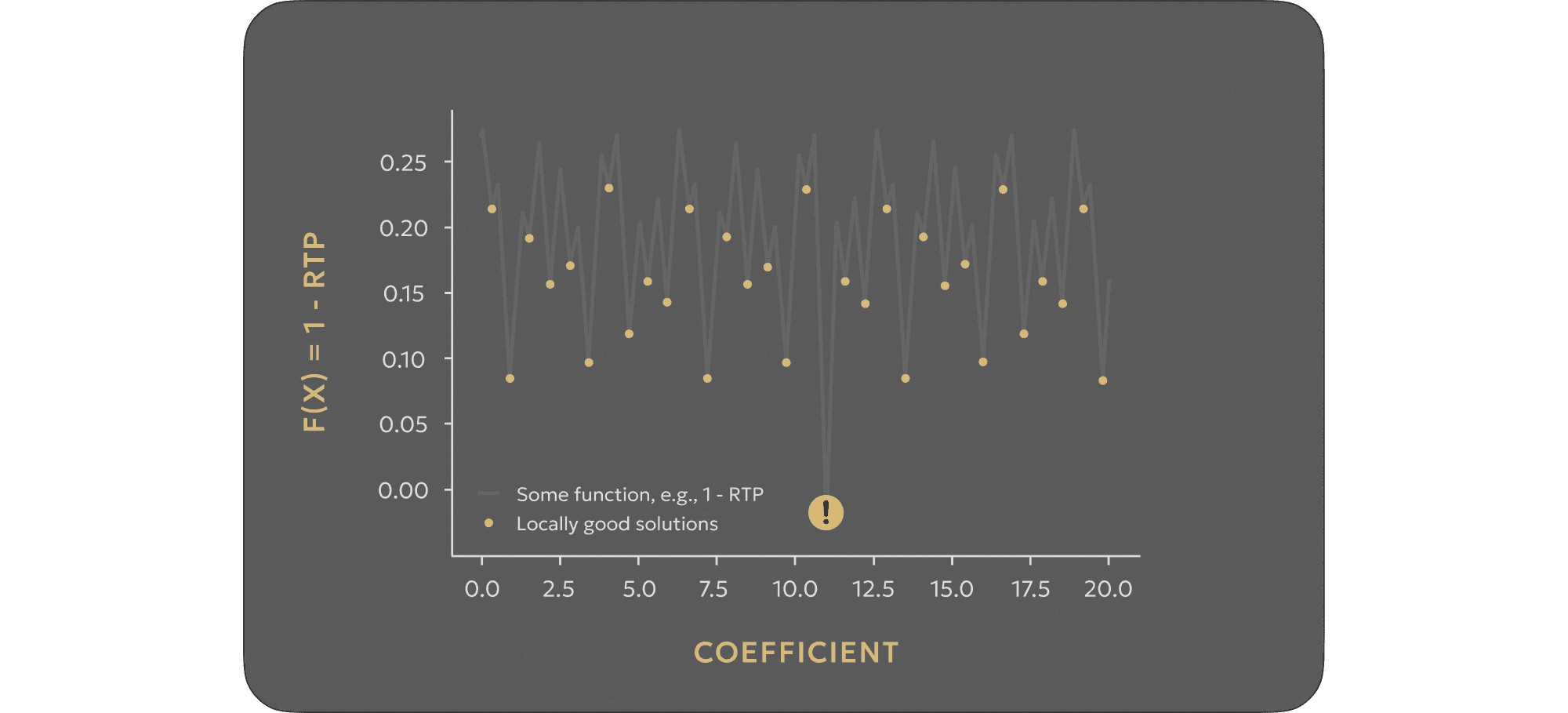
How do we detect this issue in real life? Let us try to think like a player. Our goal is to increase our wealth with a limited budget for bets. This sounds like an optimization problem: we have something controllable (for example, bet size, coefficient choice, bet type choice, sets of numbers for lottery games, etc.) and we want to maximize or minimize something (for example, to maximize the RTP or to minimize the losses)[3].

Smart Monitoring System Architecture for iGaming

Since we don't want to lose real money and since we have access to the game's software services, we cannot make real bets but simulated ones (for example, using test currencies or test environments). The monitoring system implementing algorithm vulnerability detection can be implemented in different ways:

Real-time Bot Simulation

In real-time by a bot with the possibility of making test bets (once a bot obtains RTP > 1 over a long distance, alerts are triggered, and the game can be stopped). This approach supports continuous real-time monitoring of game performance and security, and utilizes automated game testing to monitor game behavior continuously.

Scheduled Testing with Historical Data

With some periodicity using a scheduler (for example, Apache Airflow) and historical data, different algorithms can be implemented as DAGs and called, for example, every hour. This method allows for systematic and automated game testing with genetic algorithms using historical patterns. In particular, systematic genetic algorithm game testing ensures vulnerabilities are caught early, strengthening the overall reliability of antifraud mechanisms.

Pre-production Antifraud Simulations

At the test stage, before publishing the game for production, Developers can implement the simulation on the game with test bets and publish the game into production only if an RTP > 1 has not been obtained over a long distance. This preventive approach ensures robust iGaming genetic algorithm validation before release.

With smart monitoring systems, vulnerability detection can be improved before the game is released to production. In all the above-mentioned cases, we can solve the problem mathematically by applying an algorithm to find the best options and then observing whether it was possible to gain RTP > 1.

At Notix.Games™, we carefully test each of our games mathematically before and after deploying the games into production, taking into account different possible live-case scenarios. Moreover, finding the parameters of the game corresponding to the target RTP is a complex multidimensional optimization problem that is successfully solved by efficient parallel optimization algorithms. Then, we deeply study the statistical properties of the obtained mathematical model, trying to improve user experience and increase income. Finally, the application of smart antifraud simulations guarantees stability, robustness against fraud issues, and compliance with regulatory requirements.

But how do we solve such a challenging problem? That is where nature inspired algorithms come into play!

Real-World Applications of Optimization Algorithms in iGaming Antifraud

One of the main ideas to prevent iGaming antifraud consists of implementing a smart monitoring system in one of the following ways:

• One way to apply the above-mentioned algorithms is to implement a smart system with the possibility of making test bets (using test currency or a test environment) on the fly. In this case, the "bot" will make test bets during several game editions (different bets can be made on the same game edition to fulfill the population property of the algorithms). After that, the average or total RTP values are calculated and used as the goodness measure for different bet setups (for example, as the brightness for the Firefly algorithm). Once RTP > 1 has been obtained, some alerts or even automatic stopping of the game can be executed.
• Other ways to apply the algorithms consist of implementing the algorithms using available historical data. In this case, simulation of bets can be made using historical data of game results. This model can be implemented using schedulers like Apache Airflow: one can implement the DAGs with different algorithms and start them, for example, every hour.
• Finally, the algorithms can be implemented at the testing stage before starting the games in production. For example, once the game is ready to be published in production, the monitoring system using the described algorithms can be launched.

Obviously, this approach does not substitute for all other checks and monitoring. However, its main advantage is a different perspective: we look at the games and try to find vulnerabilities as players would.

Nature-Inspired Metaheuristic Algorithms

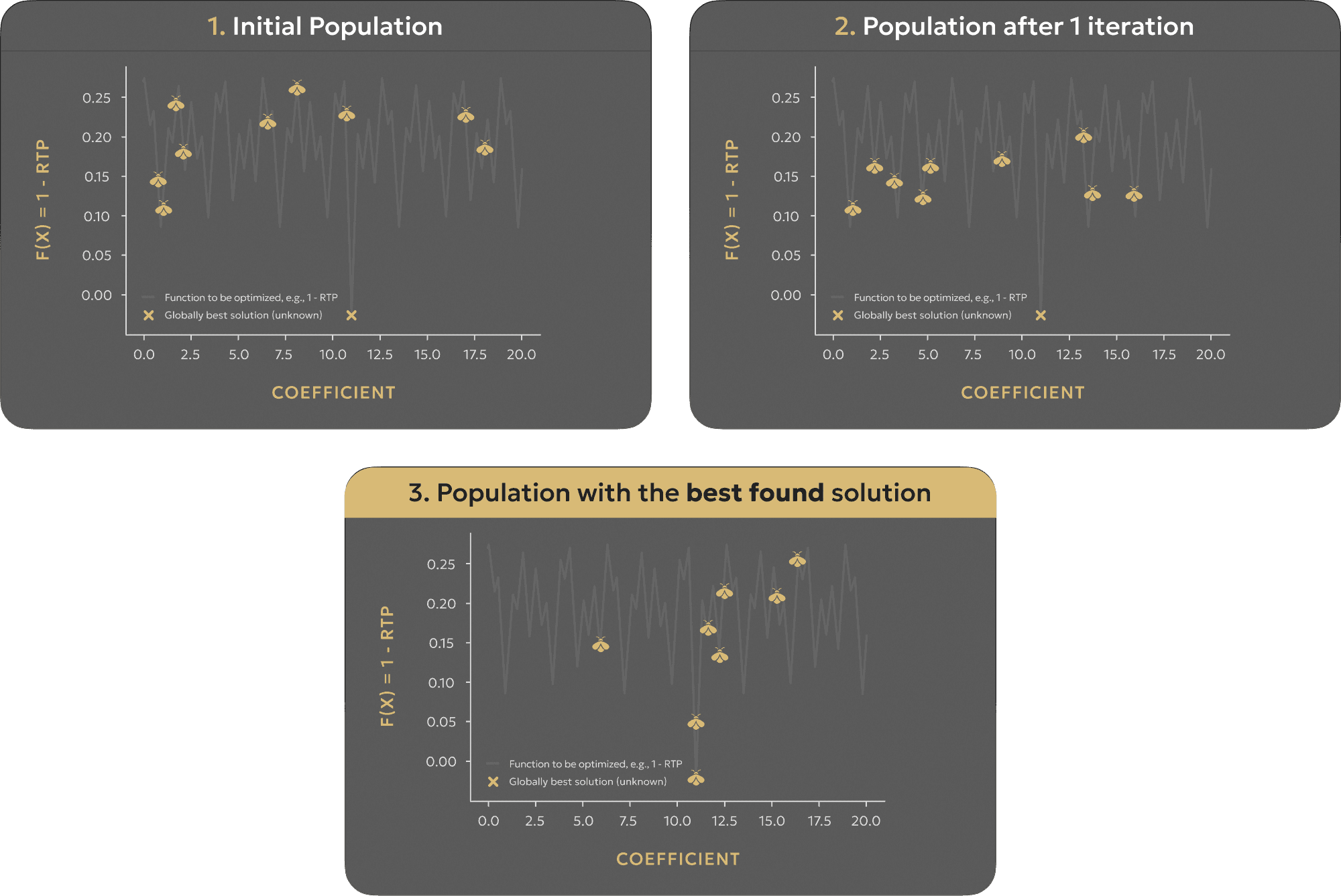
In simple terms, nature-inspired metaheuristic algorithms usually generate a random population of objects within the search space (initial population) and then balance between exploitation (local improvement of the current best solutions) and exploration (global search for better solutions) of the search space, moving the population towards better positions, similarly to swarm intelligence. Every object within the population is a possible choice of controllable parameters (there can be more than one controllable parameter; for example, we can find both good bet size and bet coefficient). We can estimate every object's fitness (or goodness): for example, what value of RTP we obtain over a long distance using this set of parameters.

Such metaheuristic algorithms usually do not have strong theoretical convergence properties (thus, they are called heuristic algorithms). Still, they are inspired by natural behavior (for example, the behavior of a bee colony in search of food sources, the flashing behavior of fireflies, the movement of a school of fish, or even evolution at different levels: genotype or phenotype). Every object in the population moves and behaves in the search space similarly to the objects in the respective natural population (for example, similarly to fireflies in the forest or to chromosomes in long-distance evolution).

Why are these algorithms better at iGaming antifraud than other optimization algorithms (for example, deterministic ones)? The answer is simple: genetic algorithms in games almost do not require any special properties of the objective function. They can be used for almost any kind of problem due to their generality. The function to be optimized can be continuous, discrete, or mixed. It can be weakly defined (for example, what does "long distance" mean mathematically?), the parameters can be of different natures, etc. Nature-inspired metaheuristic algorithms can be applied similarly without any problem in all these cases.

These algorithms usually have a set of control parameters (population size, randomness parameters, parameters controlling exploitation and exploration balance, etc.). It can be difficult to set the parameters optimally, but these algorithms are meta-heuristic, which means they can be applied to themselves to auto-tune control parameters. Solving the problems becomes easy: just send the population of "bees," "fireflies," "chromosomes," etc., into the search space, watch how they move, and find the best options.

Technical details and source code of the algorithms are not presented here to improve readability. Still, many external resources describe these algorithms well (e.g., Wikipedia) as well as algorithms themselves representing nature-inspired behaviors in different ways (Genetic Algorithm, Fireflies, Artificial Bee Colony, Ants Algorithm, Cuckoo Search, Differential Evolution, Simulated Annealing, Particle Swarm Optimization, etc.). These metaheuristic algorithms enhance the efficiency of game testing across multiple scenarios. Let us briefly describe two different algorithms for the paper's self-consistency.

Genetic Algorithm (GA)

The GA in games works on a population consisting of some solutions (called individuals) within the search space. Each individual solution has a chromosome, which is represented as a set of parameters (features) that define the individual (for example, bet size, bet type, coefficient, risk value or probability, set of chosen numbers in a lottery game, etc.).

Each chromosome has a set of genes. Each gene is represented as a string of 0s and 1s. In other words, the set of features is encoded into a binary format. So, each chromosome (or individual) has two representations: genotype (encoded set of genes or binary string) and phenotype (physical representation or decoded real-value features).

Genetic algorithms in games enable efficient search for optimal configurations of these features by applying two main mechanisms to generate a new population of individuals from the current one: crossover and mutation. Both mechanisms work on the genotype level (i.e., with binary numbers).

Crossover takes two individuals selected randomly based on their quality (better solutions are more likely to be selected) and generates two child solutions from them in a certain way. The simplest way to generate two child individuals from the parents is shown in Fig. 2. With some probability, we take the children as new individuals in the parents' place (otherwise, the parents remain unchanged).

Mutation randomly alternates individual bits of the chromosomes with a certain probability, introducing variation into the population.

Fig 2:

The main idea of the algorithm is to create new generations of individuals from the previous ones based on their fitness, similarly to natural evolution: individuals with certain better properties have a higher probability of surviving and transferring their genes, while individuals with worse properties (regarding the solving problem) have fewer chances of surviving (but they can survive and change due to some randomness of the algorithm).

Firefly Algorithm (FA)

The Firefly Algorithm is another population-based algorithm where every element of the population (a firefly) represents again the set of controllable features or parameters (coefficient, bet size, set of numbers in a lottery game, etc.). The algorithm simulates the movement of the population of fireflies within the search space (see Fig. 3).

Fig 3:

Every "firefly" has its brightness associated with the value of the objective function (function to be minimized or maximized). Better solutions (sets of controllable parameters or features) are represented by brighter fireflies. Fireflies attract each other based on their brightness, but the attractiveness decreases with the distance between two fireflies: a firefly with very high brightness located far from some other firefly can be less attractive to it than some other one that is less bright but located closer.

Fireflies move towards each other based on their attractiveness: less attractive fireflies move towards more attractive ones. However, the movement is not strictly deterministic, as there is always some randomness added (random noise added to the movement).

One of the main differences of this algorithm with respect to others (for example, with GA) consists of the convergence to several local solutions simultaneously. The algorithm better explores the search space and can be applied to complex optimization problems of any kind.

Conclusion

Nature-inspired metaheuristic algorithms are powerful for solving challenging real-life problems, including iGaming antifraud problems. They can be applied in many different ways to avoid resource losses due to vulnerabilities and fraudulent behavior.

All the above-mentioned ideas represent additional ways to improve antifraud systems in the iGaming industry. These mechanisms, including genetic algorithms in games, can be strong instruments for improving game stability and safety, leading to a better player experience as well. Ultimately, automated game testing should be considered an essential part of the overall game testing and QA process, ensuring continuous monitoring and long-term reliability.

Notes:

[1] All cases described in this article have illustrative purposes only. These cases are simplified to improve readability: real-life applications can be much more difficult and require special analysis. This article is not meant to teach players how to cheat; all examples are for illustration only. However, the main idea of the paper, as well as the described techniques, can be applied for almost any kind of similar problem.

[2] Crash games are used here as an example, since the approach is easiest to illustrate with a single simple parameter.

[3] A maximization problem is always equivalent mathematically to a minimization problem by just changing the sign of the objective function. For example, maximization of the RTP is the same as minimization of the -RTP or 1 - RTP. For this reason, the problem of minimizing something is usually considered without loss of generality.